- Oct 9, 2005
- 4,767
- 435
- 126
Hi,
I work in the IT department of a company full of engineers, but I'm not an engineer myself. I'm currently employed in the company as a consultant for SAP ERP currently used by my organization. Since I joined this company, I have developed an interest in learning mathematics and science (as a hobby, not for work). Right now I'm learning trigonometry using Michael Corral Trigonometry textbook. One of the exercises in the book stumps me very much and I have been hunting for a solution to it.
The book exercise says r = 0.944 in the solutions section. However I'm not getting how to derive the same. Here is the exercise as described in the text book :
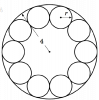
1.3.25 A manufacturer needs to place ten identical ball bearings against the inner side of a circular container such that each ball bearing touches two other ball bearings, as in the picture on the right. The (inner) radius of the container is 44 cm.
(a) Find the common radius r of the ball bearings.
(b) The manufacturer needs to place a circular ring\\inside the container. What is the largest possible (outer) radius of the ring such that it is not on top\\of the ball bearings and its base is level with the\\base of the container?
I know this is elementary and basic. But it has been long since I have practiced mathematics since school and college. By the way, I'm 43 years old and I'm ashamed of being a maths brainlet. Please be assured this is not my school homework or anything.
Please help.
I work in the IT department of a company full of engineers, but I'm not an engineer myself. I'm currently employed in the company as a consultant for SAP ERP currently used by my organization. Since I joined this company, I have developed an interest in learning mathematics and science (as a hobby, not for work). Right now I'm learning trigonometry using Michael Corral Trigonometry textbook. One of the exercises in the book stumps me very much and I have been hunting for a solution to it.
The book exercise says r = 0.944 in the solutions section. However I'm not getting how to derive the same. Here is the exercise as described in the text book :

1.3.25 A manufacturer needs to place ten identical ball bearings against the inner side of a circular container such that each ball bearing touches two other ball bearings, as in the picture on the right. The (inner) radius of the container is 44 cm.
(a) Find the common radius r of the ball bearings.
(b) The manufacturer needs to place a circular ring\\inside the container. What is the largest possible (outer) radius of the ring such that it is not on top\\of the ball bearings and its base is level with the\\base of the container?
I know this is elementary and basic. But it has been long since I have practiced mathematics since school and college. By the way, I'm 43 years old and I'm ashamed of being a maths brainlet. Please be assured this is not my school homework or anything.
Please help.




